Arbeitsblatt 1 zu M 3

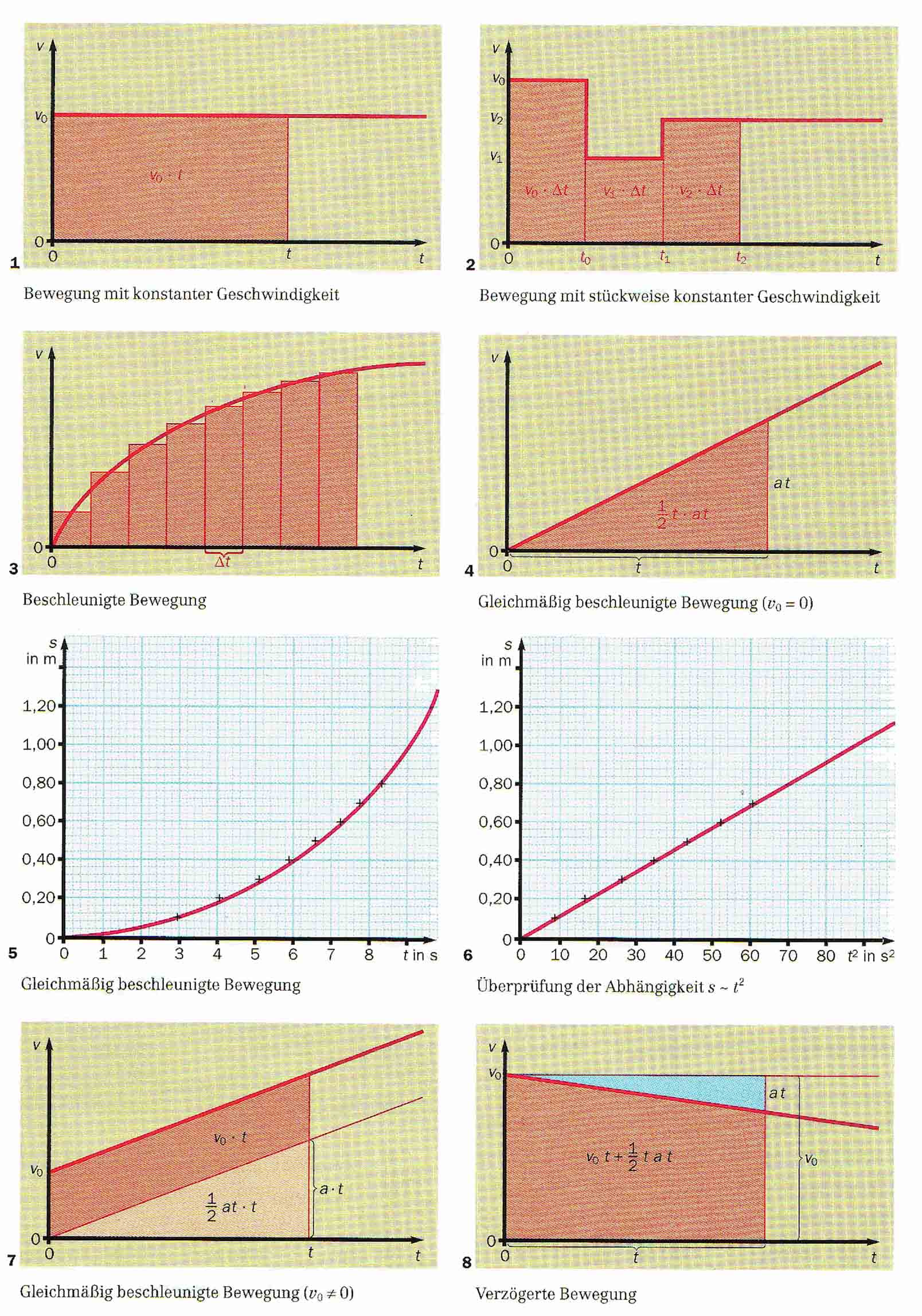
Die Geraden in v(t)-Diagrammen von gleichmäßig beschleunigten Bewegungen (Bild 7) können durch Gleichungen der Form v(t) = v₀ + a t beschrieben werden. Dabei ist v₀ die Geschwindigkeit zum Zeitpunkt t=0s . v(t) gibt dann die Geschwindigkeit in einem beliebigen Zeitpunkt an. Besonders einfach wird die Gleichung, wenn aus dem Stand gestartet wird, wenn der Körper zum Zeitpunkt 0 gerade die Geschwindigkeit v₀=0 m/s hat. Dann gilt: v(t)=a t . Die Gerade im v(t)-Diagramm ist eine Ursprungsgerade, v ist proportional zu t.

Welchen Weg hat der Körper bei einer gleichmäßig beschleunigten Bewegung zu einem beliebigen Zeitpunkt zurückgelegt? Im einfachsten Fall gilt a=0 m/s². Für eine solche Bewegung mit konstanter Geschwindigkeit v₀ ergibt sich im v(t)-Diagramm eine Parallele zur Zeitachse (Bild 1). Zu einem beliebigen Zeitpunkt gilt s=v₀ t. Der Flächeninhalt des Rechtecks ist ein Maß für den zur Zeit t zurückgelegten Weg. Auch wenn sich die Geschwindigkeit wie in Bild 2 ändert, entspricht jede Teilfläche einem Teil des zurückgelegten Weges. Die Gesamtfläche entspricht dem gesamten Weg. Wenn sich die Geschwindigkeit kontinuierlich ändert, kann man die Zeit in Gedanken in so kleine Abschnitte zerlegen, dass sich die Geschwindigkeit in so kleinen Zeiten kaum ändert (Bild 3). Daher entspricht jetzt die Fläche unter dem v(t)-Graphen der zurückgelegten Strecke. Diese Fläche ist bei einer gleichmäßig beschleunigten Bewegung leicht zu berechnen (Bild 4). Sie beträgt ½ t ( a t ) . Also gilt: s(t) = ½ a t² .

Beim Eintragen von Messwerten s und t einer gleichmäßig beschleunigten Bewegung (z.B.: beim Abrollen einer Kugel auf einer schiefen Ebene) erhält man ein Diagramm wie in Bild 5. Es ergibt sich eine Kurve, die Teil einer Ursprungsparabel sein könnte. Es gibt zwei Möglichkeiten, diese Vermutung zu bestätigen:

• Man berechnet erstens für jede Messung den Quotienten s/t² . Er muss konstant und gleich dem halben Wert der Beschleunigung sein.

• Zweitens gilt: Dass s/t² konstant ist, ist gleichbedeutend damit, dass s zu t² proportional ist. Man überprüft also, ob sich im s(t²)-Diagramm eine Ursprungsgerade ergibt.

Bild 6 zeigt zu Bild 5 das s(t²)-Diagramm. Die Steigung entspricht dem halben Wert der Beschleunigung. Unsere Überlegungen werden bestätigt.

Lautet die Gleichung für die Geschwindigkeit v = v₀ + a t , so kann die Fläche unter dem Graphen in ein Dreieck und ein Parallelogramm zerlegt werden (Bild 7). Die Fläche des Parallelogramms kann berechnet werden als v₀ t . Also gilt insgesamt: s(t) = ½ a t² + v₀ t .

Bei Bewegungen mit negativer Beschleunigung (verzögerte Bewegung) wie in Bild 8 muss die Fläche des kleinen Dreiecks von der Rechteckfläche abgezogen werden. Mit a ist auch ½ a t² negativ. Daher beschreibt auch hier der Ausdruck s(t) = ½ a t² + v₀ t die restliche Fläche und damit den zurückgelegten Weg.